Function Is one of the most important mathematical concepts. Function - Variable Dependency at from variable x if each value NS matches a single value at... Variable NS called the independent variable or argument. Variable at called the dependent variable. All values of the independent variable (variable x) form the domain of the function. All values that the dependent variable (variable y), form the range of values of the function.
Function graph the set of all points of the coordinate plane is called, the abscissa of which are equal to the values of the argument, and the ordinates are equal to the corresponding values of the function, that is, the values of the variable are plotted along the abscissa axis x, and the ordinate represents the values of the variable y... To plot a function graph, you need to know the properties of the function. The main properties of the function will be discussed later!
To graph a function, we recommend using our program - Graphing Functions Online. If you have any questions while studying the material on this page, you can always ask them on our forum. Also on the forum you will be helped to solve problems in mathematics, chemistry, geometry, probability theory and many other subjects!
Basic properties of functions.
1) Function domain and function domain.
Function scope is the set of all valid valid argument values x(variable x) for which the function y = f (x) defined.
The range of values of a function is the set of all real values y that the function accepts.
In elementary mathematics, functions are studied only on the set of real numbers.
2) Function zeros.
Function zero is an argument value at which the function value is equal to zero.
3) Intervals of constancy of function.
The intervals of constant sign of a function are such sets of argument values on which the function values are only positive or only negative.
4) Monotonicity of function.
An increasing function (in a certain interval) is a function for which a larger value of the argument from this interval corresponds to a larger value of the function.
Decreasing function (in a certain interval) - a function for which the larger value of the argument from this interval corresponds to the smaller value of the function.
5) Parity (odd) function.
An even function is a function whose domain of definition is symmetric about the origin and for any NS from the domain of definition, the equality f (-x) = f (x)... The graph of an even function is symmetric about the ordinate axis.
An odd function is a function whose domain of definition is symmetric about the origin and for any NS from the domain of definition, the equality f (-x) = - f (x). The graph of an odd function is symmetric about the origin.
6) Limited and unlimited functions.
A function is called bounded if there is a positive number M such that | f (x) | ≤ M for all values of x. If there is no such number, then the function is unlimited.
7) Periodicity of the function.
A function f (x) is periodic if there exists a nonzero number T such that for any x f (x + T) = f (x). This smallest number is called the period of the function. All trigonometric functions are periodic. (Trigonometric formulas).
Having studied these properties of the function, you can easily explore the function and, by the properties of the function, you can build a graph of the function. Also look at the material about the truth table, multiplication table, periodic table, table of derivatives and table of integrals.
Function zeros
What are function zeros? How to determine the zeros of a function analytically and from a graph?
Function zeros are the argument values at which the function is zero.
To find the zeros of the function given by the formula y = f (x), you need to solve the equation f (x) = 0.
If the equation has no roots, the function has no zeros.
1) Find the zeros of the linear function y = 3x + 15.
To find the zeros of the function, solve the equation 3x + 15 = 0.
Thus, the zero of the function y = 3x + 15 - x = -5.
2) Find the zeros of the quadratic function f (x) = x²-7x + 12.
To find the zeros of the function, we solve the quadratic equation
Its roots x1 = 3 and x2 = 4 are the zeros of this function.
3) Find the zeros of the function
The fraction is meaningful if the denominator is nonzero. Therefore, x²-1 ≠ 0, x² ≠ 1, x ≠ ± 1. That is, the domain of definition of this function (ODZ)
From the roots of the equation x² + 5x + 4 = 0 x1 = -1 x2 = -4, only x = -4 is included in the domain of definition.
To find the zeros of a function given graphically, it is necessary to find the points of intersection of the graph of the function with the abscissa axis.
If the graph does not cross the Ox axis, the function has no zeros.
the function, the graph of which is shown in the figure, has four zeros -
In algebra, the problem of finding the zeros of a function occurs both as an independent task and when solving other problems, for example, when studying a function, solving inequalities, etc.
www.algebraclass.ru
Function zeros rule
Basic concepts and properties of functions
The rule (law of) conformity. Monotone function .
Limited and unlimited functions. Continuous and
discontinuous function . Even and odd functions.
Periodic function. Function period.
Function zeros . Asymptote .
Domain and range of values of the function. In elementary mathematics, functions are studied only on the set of real numbers R ... This means that the argument of a function can only take valid values for which the function is defined, i.e. it also only takes valid values. A bunch of X all valid valid argument values x for which the function y = f (x) is defined, called function scope... A bunch of Y all valid values y that the function takes is called function range... Now we can give a more precise definition of the function: the rule (law of) correspondence between sets X and Y , according to which for each element from the set X you can find one and only one element from the set Y is called the function .
It follows from this definition that a function is considered given if:
- the scope of definition of the function is set X ;
- the range of values of the function is set Y ;
- the rule (law) of conformity is known, and such that for each
argument values, only one function value can be found.
This requirement for unambiguous functions is mandatory.
Monotonic function.
If for any two values of the argument x 1 and x 2 from condition x 2 > x 1 follows f (x 2) > f (x 1), then the function f (x) is called increasing; if for any x 1 and x 2 from condition x 2 > x 1 follows f (x 2) 
The function depicted in Figure 3 is limited, but not monotonic. The function in Figure 4 is just the opposite, monotonous but unlimited. (Explain this, please!).
Continuous and discontinuous functions. Function y = f (x) is called continuous at the point x = a, if:
1) the function is defined at x = a, i.e. f (a) exist;
2) exists finite limit lim f (x) ;
If at least one of these conditions is not met, then the function is called discontinuous at the point x = a .
If the function is continuous in of all points of its domain of definition then it is called continuous function.
Even and odd functions. If for any x from the scope of the function definition takes place: f (— x) = f (x), then the function is called even; if it takes place: f (— x) = — f (x), then the function is called odd... Even function graph symmetric about the Y-axis(Fig. 5), a graph of an odd function Sim metric with respect to the origin(fig. 6).
Periodic function. Function f (x) — periodic if there is such nonzero number T what for any x from the scope of the function definition takes place: f (x + T) = f (x). Such the fewest the number is called period of function... All trigonometric functions are periodic.
EXAMPLE 1. Prove that sin x has a period of 2.
Solution. We know that sin ( x + 2 n) = sin x, where n= 0, ± 1, ± 2, ...
Therefore, Appendix 2 n to the sine argument is not
changes its value e. Is there another number with such
Let's pretend that P- such a number, i.e. equality:
valid for any value x... But then it has
place and at x= / 2, i.e.
sin (/ 2 + P) = sin / 2 = 1.
But according to the reduction formula sin (/ 2 + P) = cos P... Then
from the last two equalities it follows that cos P= 1, but we
we know that this is true only when P = 2 n... Since the smallest
a nonzero number of 2 n is 2, then this number
and there is a period sin x... It can be proved similarly that 2
is the period for cos x .
Prove that the functions tan x and cot x have a period.
EXAMPLE 2. What number is the period of the function sin 2 x ?
Solution. Consider sin 2 x= sin (2 x + 2 n) = sin [2 ( x + n) ] .
We see that adding n to the argument x, does not change
function value. Smallest nonzero number
from n is, therefore, this is the period sin 2 x .
Function zeros. The value of the argument at which the function is equal to 0 is called zero ( root) function... A function can have multiple zeros. For example, the function y = x (x + 1) (x- 3) has three zeros: x = 0, x = — 1, x= 3. Geometrically function zero – this is the abscissa of the point of intersection of the function graph with the axis NS .
Figure 7 shows a graph of the function with zeros: x = a , x = b and x = c .
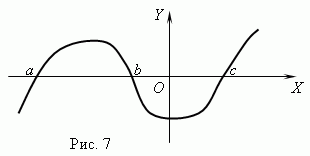
Asymptote. If the graph of a function unrestrictedly approaches some straight line at its distance from the origin, then this straight line is called asymptote.
Topic 6. "Method of intervals".
If f (x) f (x 0) at x x 0, then the function f (x) is called continuous at point x 0.
If a function is continuous at every point of some interval I, then it is called continuous in between I (interval I is called interval of continuity of the function). The graph of the function at this interval is a continuous line, which is said to be "drawn without lifting the pencil from the paper."
The property of continuous functions.
If on the interval (a; b) the function f is continuous and does not vanish, then it retains a constant sign on this interval.
This property is the basis of the method for solving inequalities with one variable - the method of intervals. Let the function f (x) be continuous on an interval I and vanish at a finite number of points of this interval. By the property of continuous functions, these points divide I into intervals, in each of which the continuous function f (x) c guards a constant sign. To determine this sign, it is enough to calculate the value of the function f (x) at any one point from each such interval. Based on this, we obtain the following algorithm for solving inequalities by the method of intervals.
The interval method for inequalities of the form
The method of intervals. Average level.
Do you want to test your strength and find out the result of how ready you are for the Unified State Exam or the OGE?
Linear function
A function of the form is called linear. Let's consider a function as an example. It is positive at 3 ″> and negative at. The point is the zero of the function (). Let us show the signs of this function on the numerical axis:
We say that "the function changes sign when passing through a point."
It can be seen that the signs of the function correspond to the position of the graph of the function: if the graph is above the axis, the sign is "", if it is below - "".
If we generalize the resulting rule to an arbitrary linear function, we get the following algorithm:
Quadratic function
I hope you remember how square inequalities are solved? If not, read the topic "Square inequalities." Let me remind you the general form of the quadratic function:.
Now let's remember what signs the quadratic function takes. Its graph is a parabola, and the function takes the sign "" when the parabola is above the axis, and "" - if the parabola is below the axis:
If the function has zeros (values at which), the parabola intersects the axis at two points - the roots of the corresponding quadratic equation. Thus, the axis is divided into three intervals, and the signs of the function alternately change when passing through each root.
Is it possible to somehow define the signs without drawing a parabola every time?
Recall that the square trinomial can be factorized:
Let's mark the roots on the axis:
We remember that the sign of a function can only change when passing through the root. We use this fact: for each of the three intervals into which the axis is divided by roots, it is enough to determine the sign of the function at only one arbitrarily chosen point: at the other points of the interval, the sign will be the same.
In our example: for 3 ″> both expressions in parentheses are positive (substitute, for example: 0 ″>). We put the sign "" on the axis:
Well, for (substitute, for example,) both parentheses are negative, which means that the product is positive:
That's what it is interval method: knowing the signs of the factors at each interval, we determine the sign of the entire product.
Consider also the cases when the function has no zeros, or only one.
If they are not there, then there are no roots. This means that there will be no "root crossing" either. This means that the function takes only one sign on the entire numerical axis. It is easy to define it by substituting it into a function.
If there is only one root, the parabola touches the axis, so the sign of the function does not change when passing through the root. What rule can we come up with for such situations?
If you factor out such a function, you get two identical factors:
And any expression squared is non-negative! Therefore, the sign of the function does not change. In such cases, we will select a root, passing through which the sign does not change, circling it with a square:
We will call such a root multiple.
The method of intervals in inequalities
Now any square inequality can be solved without drawing a parabola. It is enough only to arrange the signs of the quadratic function on the axis, and choose the intervals depending on the sign of the inequality. For example:
Let's measure the roots on the axis and place the signs:
We need the part of the axis with the sign ""; since the inequality is not strict, the roots themselves are also included in the solution:
Now consider a rational inequality - an inequality, both sides of which are rational expressions (see "Rational Equations").
Example:
All factors except one - - here are "linear", that is, they contain the variable only in the first degree. We need such linear factors to apply the method of intervals - the sign changes when passing through their roots. But the factor has no roots at all. This means that it is always positive (check it yourself), and therefore does not affect the sign of all inequality. This means that we can divide the left and right sides of the inequality into it, and thus get rid of it:
Now everything is the same as it was with square inequalities: we determine at which points each of the factors vanishes, mark these points on the axis and place signs. I would like to draw your attention to a very important fact:
In the case of an even number, we proceed in the same way as before: circle the point with a square and do not change the sign when passing through the root. But in the case of an odd number, this rule is not met: the sign will still change when passing through the root. Therefore, we do nothing additionally with such a root, as if it is not a multiple of it. The above rules apply to all odd and even degrees.
What will we write in the answer?
In case of violation of the alternation of signs, you need to be very careful, because with a lax inequality, the answer should be all filled dots... But some of the tries often stand alone, that is, they do not enter the shaded area. In this case, we add them to the answer as isolated dots (in curly braces):
Examples (decide for yourself):
Answers:
- If it is simple among the multipliers, this is the root, because it can be represented as.
.
What are function zeros? The answer is quite simple - this is a mathematical term, which means the domain of a given function, on which its value is zero. Function zeros are also called function zeros The easiest way to explain what function zeros are is with a few simple examples.
Examples of
Consider the simple equation y = x + 3. Since the zero of the function is the value of the argument at which y acquired zero, we substitute 0 in the left side of the equation:
In this case, -3 is the desired zero. There is only one root of the equation for a given function, but this is not always the case.
Let's consider another example:
Substitute 0 on the left side of the equation, as in the previous example:
Obviously, in this case there will be two zeros of the function: x = 3 and x = -3. If the equation had a third-degree argument, there would be three zeros. A simple conclusion can be made that the number of roots of the polynomial corresponds to the maximum degree of the argument in the equation. However, many functions, for example y = x 3, at first glance contradict this statement. Logic and common sense suggest that this function has only one zero - at the point x = 0. But in fact, there are three roots, they just all coincide. If you solve the equation in complex form, it becomes obvious. x = 0 in this case, the root, the multiplicity of which is 3. In the previous example, the zeros did not coincide, so they had a multiplicity of 1.
Algorithm for determining
From the examples presented, you can see how to determine the zeros of the function. The algorithm is always the same:
- Write function.
- Substitute y or f (x) = 0.
- Solve the resulting equation.
The complexity of the last point depends on the degree of the argument of the equation. When solving equations of high degrees, it is especially important to remember that the number of roots of the equation is equal to the maximum degree of the argument. This is especially true for trigonometric equations, where dividing both parts by sine or cosine leads to the loss of roots.
Equations of arbitrary degree are easiest to solve by Horner's method, which was developed specifically for finding the zeros of an arbitrary polynomial.
The value of the zeros of functions can be either negative or positive, real or lying in the complex plane, single or multiple. Or the roots of the equation may not exist. For example, the function y = 8 will not acquire zero value for any x, because it does not depend on this variable.
The equation y = x 2 -16 has two roots, and both lie in the complex plane: x 1 = 4і, x 2 = -4і.
Typical mistakes
A common mistake made by schoolchildren who have not yet fully understood what the zeros of a function are is to replace the argument (x) with zero, and not the value (y) of the function. They confidently substitute x = 0 into the equation and, proceeding from this, find y. But this is the wrong approach.
Another mistake, as already mentioned, is the reduction by sine or cosine in the trigonometric equation, which is why one or more zeros of the function are lost. This does not mean that nothing can be canceled in such equations; it is just that in further calculations it is necessary to take into account these "lost" factors.
Graphical representation
To understand what function zeros are, you can use mathematical programs such as Maple. In it, you can build a graph by specifying the desired number of points and the desired scale. The points at which the graph crosses the OX axis are the desired zeros. This is one of the fastest ways to find the roots of a polynomial, especially if its order is higher than three. So if there is a need to regularly perform mathematical calculations, find the roots of polynomials of arbitrary degrees, build graphs, Maple or a similar program will be simply indispensable for performing and checking calculations.
In which it takes on a null value. For example, for a function defined by the formula
Is zero because
.Function zeros are also called rooted function.
The concept of zeros of a function can be considered for any functions whose range of values contains zero or zero element of the corresponding algebraic structure.
For a real variable function, the zeros are the values at which the function graph crosses the abscissa axis.
Finding the zeros of a function often requires the use of numerical methods (for example, Newton's method, gradient methods).
One of the unsolved mathematical problems is finding the zeros of the Riemann zeta function.
Polynomial root
see also
Literature
Wikimedia Foundation. 2010.
See what "Function zero" is in other dictionaries:
The point where the given function f (z) vanishes; thus, N. f. f (z) is the same as the roots of the equation f (z) = 0. For example, the points 0, π, π, 2π, 2π, ... are the zeros of the function sinz. Zeros of the analytical function (See Analytical ... ...
Zero function, zero function ... Spelling dictionary-reference
This term has other meanings, see Zero. It is necessary to move the content of this article to the article "Zero function". You can help the project by combining articles. If it is necessary to discuss the feasibility of unification, replace this ... Wikipedia
Or C string (from the name of the C language) or ASCIZ string (from the name of the assembler directive .asciz) is a way of representing strings in programming languages, in which instead of introducing a special string type, an array of characters is used, and the end is ... ... Wikipedia
In quantum field theory, the accepted (jargon) name for the property of vanishing of the coupling constant renormalization factor where g0 is the bare coupling constant from the interaction Lagrangian, phys. coupling constant dressed with interaction. Equality Z ... Physical encyclopedia
Null mutation n-allele- Zero mutation, n. allele * null mutation, n. allele * null mutation or n. allel or silent a. a mutation leading to a complete loss of function in the DNA sequence in which it occurred ... Genetics. encyclopedic Dictionary
The statement in the theory of probability that any event (the so-called residual event), the onset of which is determined only by arbitrarily remote elements of a sequence of independent random events or random variables, has ... ... Encyclopedia of mathematics
1) A number with the property that any (real or complex) number does not change when added to it. It is denoted by the symbol 0. The product of any number by N. is equal to N.: If the product of two numbers is equal to N., then one of the factors ... Encyclopedia of mathematics
Functions defined by relationships between independent variables that are not permitted relative to the latter; these ratios are one of the ways to define the function. For example, the relation x2 + y2 1 = 0 sets the N. f. ... Great Soviet Encyclopedia
Argument values z at which f(z) vanishes called. zero point, i.e. if f(a) = 0, then a - zero point.
Def. Dot but called order zeron
, if
FKP can be represented as f(z) =, where 
analytic function and 
0.
In this case, in the expansion of the function in the Taylor series (43), the first n coefficients are equal to zero
=
=
Etc. Determine the order of zero for 
and (1 –cos z) at z
=
0
=
=
zero 1 order
1 - cos z
=
=
zero 2nd order
Def. Dot z
=
called infinitely distant point and zero function f(z), if f(
) = 0. Such a function can be expanded in a series in negative powers z
: f(z)
=
... If
the first n
coefficients are equal to zero, then we arrive at zero order n
at an infinitely distant point: f(z)
= z
-
n
.
Isolated singular points are divided into: a) removable singular points; b) poles of ordern; in) essential points.
Dot but called removable singular point function f(z) if for z 
a
lim f(z)
= with - finite number .
Dot but called pole of ordern
(n
1) functions f(z) if the inverse function 
=
1/
f(z) has a zero of order n at the point but. Such a function can always be represented as f(z)
=
, where 
- analytical function and 
.
Dot but called essential point function f(z) if for z 
a
lim f(z) does not exist.
Laurent series
Consider the case of an annular convergence domain r < | z 0 – a| < R centered at point but for function f(z). Let's introduce two new circles L 1 (r) and L 2 (R) near the boundaries of the ring with the point z 0 in between. Let's make a cut of the ring, connect the circles along the edges of the cut, go to the simply connected region and in
integral Cauchy formula (39), we obtain two integrals with respect to the variable z
f(z 0)
=
+
,
(42)
where the integration goes in opposite directions.
For the integral over L 1 the condition | z 0 – a | > | z – a |, and for the integral over L 2 converse condition | z 0 – a | < | z – a |. Therefore, the factor 1 / ( z – z 0) we expand in a series (a) in the integral over L 2 and in series (b) in the integral over L one . As a result, we obtain the decomposition f(z) in the annular region in Laurent series in positive and negative powers ( z 0 – a)
f(z 0)
=
A n
(z 0 - a) n
(43)
where A n
=
=
;A -n
=
Expansion in positive powers (z 0 - but) called. the right part Laurent series (Taylor series), and the expansion in negative powers is called. main part Laurent series.
If inside the circle L 1, there are no singular points and the function is analytic, then in (44) the first integral is equal to zero by the Cauchy theorem, and only the correct part remains in the expansion of the function. Negative powers in expansion (45) appear only when analyticity is violated within the inner circle and serve to describe the function near isolated singular points.
To construct the Laurent series (45) for f(z), one can calculate the expansion coefficients by the general formula or use the expansions of the elementary functions included in f(z).
The number of terms ( n) of the main part of the Laurent series depends on the type of singular point: disposable singular point
(n
=
0)
; essential point
(n 
);
polen- oh order(n
-
finite number).
and for f(z)
=
dot z
= 0 removable singular point, since the main part is not. f(z)
=
(z
-
) = 1 -
b) For f(z)
=
dot z
= 0 -
1st order pole
f(z)
=
(z
-
) =
-
c) For f(z) = e 1 / z dot z = 0 - essential point
f(z)
=
e 1 /
z =
If f(z) is analytic in the area D with the exception of m isolated singular points 
and | z 1 |
< |z 2 |
< . . . < |z m| , then when expanding the function in powers z the whole plane is split into m+ 1 ring | z i |
< | z
| < | z i+ 1 | and the Laurent row has a different look for each ring. Expanding in powers ( z
–
z i
) the domain of convergence of the Laurent series is the circle | z
–
z i
| < r, where r
- the distance to the nearest special point.
Etc. Expand the function f(z)
=
in Laurent's row by degrees z and ( z
-
1).
Solution. We represent the function in the form f(z)
= - z 2
... We use the formula for the sum of a geometric progression 
... In the circle | z |< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . ... ... , i.e. decomposition contains only correct part. Let's go to the outer area of the circle | z | > 1. We represent the function as 
, where 1 / | z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
Because , the expansion of the function in powers ( z
-
1) has the form f(z)
= (z
-
1) -1
+ 2 + (z
-
1) for everyone 
1.
Etc. Expand the Laurent function f(z)
=
:
a) by degrees z in a circle | z|
< 1; b)
по степеням z
ring 1<
|z|
< 3 ; c)
по степеням (z
–
2) .Solution. We expand the function into simple fractions
=
=
+
=
.
From the conditions z
=1
A
= -1/2 , z
=3
B
= ½.
but) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], for | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), for 1< |z|
< 3.
with) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, for | 2 - z|
< 1
It is a circle of radius 1 centered at the point z = 2 .
In some cases, power series can be reduced to a set of geometric progressions, and after that it is easy to determine the region of their convergence.
Etc. Investigate the convergence of the series
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Solution. This is the sum of two geometric progressions with q 1
=
, q 2 = (). From the conditions of their convergence it follows 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
The mathematical representation of a function clearly shows how one quantity completely determines the value of another quantity. Traditionally, numeric functions are considered that associate one number with another. The zero of a function is usually called the value of the argument at which the function vanishes.
Instructions
1. In order to find the zeros of the function, you need to equate its right side to zero and solve the resulting equation. Imagine you are given a function f (x) = x-5.
2. To find the zeros of this function, take and equate its right side to zero: x-5 = 0.
3. Having solved this equation, we get that x = 5 and this value of the argument will be the zero of the function. That is, when the argument is 5, the function f (x) vanishes.
Under the view function in mathematics, they understand the relationship between the elements of sets. More correctly, this is a "law" according to which the entire element of one set (called the domain of definition) is associated with a certain element of another set (called the domain of values).
You will need
- Knowledge in algebra and mathematical overview.
Instructions
1. The values function it is a kind of area, values from which the function can take. Let's say the value range function f (x) = | x | from 0 to infinity. To discover meaning function at a certain point you need to substitute for the argument function its numerical equivalent, the resulting number will be meaning m function... Let the function f (x) = | x | - 10 + 4x. Find meaning function at the point x = -2. Substitute the number -2 instead of x: f (-2) = | -2 | - 10 + 4 * (- 2) = 2 - 10 - 8 = -16. I.e meaning function at point -2 is -16.
Note!
Before looking for the value of a function at a point, make sure that it is within the scope of the function.
Useful advice
By a similar method, it is possible to detect the value of a function of several arguments. The difference is that instead of one number, you will need to substitute several - according to the number of arguments of the function.
The function represents the established relationship of the variable y to the variable x. Moreover, all the value of x, called the argument, corresponds to the exceptional value of the y - function. In a graphical form, a function is depicted in a Cartesian coordinate system in the form of a graph. The points of intersection of the graph with the abscissa axis, on which the arguments x are laid, are called the zeros of the function. Finding valid zeros is one of the tasks of finding a given function. In this case, all admissible values of the independent variable x are taken into account, which form the domain of definition of the function (OOF).
Instructions
1. The zero of a function is such a value of the argument x at which the value of the function is equal to zero. However, only those arguments that are included in the definition of the function under study can be zeros. That is, in such a lot of values for which the function f (x) is meaningful.
2. Write down the given function and equate it to zero, say f (x) = 2x? + 5x + 2 = 0. Solve the resulting equation and find its real roots. Quadratic roots are calculated with support for finding the discriminant. 2x? + 5x + 2 = 0; D = b? -4ac = 5? -4 * 2 * 2 = 9; x1 = (-b +? D) / 2 * a = (-5 + 3) / 2 * 2 = -0.5; x2 = (-b-? D) / 2 * a = (-5-3) / 2 * 2 = -2. Thus, in this case, two roots of the quadratic equation are obtained, corresponding to the arguments of the initial function f (x).
3. Check all detected values of x for belonging to the domain of the specified function. Find OOF, for this, check the initial expression for the presence of roots of an even power of the form? F (x), for the presence of fractions in a function with an argument in the denominator, for the presence of logarithmic or trigonometric expressions.
4. Considering a function with an expression under an even root, take as the domain of definition all arguments x, the values of which do not turn the radical expression into a negative number (on the contrary, the function does not make sense). Check if the found zeros of the function fall within a certain range of valid values of x.
5. The denominator of a fraction cannot vanish, therefore, exclude those arguments x that lead to such a result. For logarithmic quantities, only those values of the argument should be considered for which the expression itself is greater than zero. The zeros of the function that turn the sub-logarithmic expression to zero or a negative number must be discarded from the final total.
Note!
When finding the roots of the equation, unnecessary roots may appear. It is easy to check this: it is enough to substitute the received value of the argument into the function and make sure whether the function vanishes.
Useful advice
Occasionally a function is not expressed in an obvious way through its argument, then it is easy to know what this function is. An example of this is the equation of a circle.
